So, a while back, I applied to be a teaching assistant at a Maths school. This Maths school runs on Saturdays, and was originally meant to be an enrichment program: for kids to get ahead, or to just--yeah, "enrich" their understanding of Mathematics.
I want to write a paper on how awesome Math is.
It's just, that's been done so many times already; and, from what I've read, unsatisfactorily. I'm reading Mathematical Sorcery in my spare time right now. It's good, I guess; but there's this one section that tries to induce the reader to look at an equation as one might look at a piece of art, and the author describes how he gets tingles down his spine. I'm not a writer, but I think that was unnecessarily personal; if something is awesome, the reader can figure it out for himself (gender-inclusive "himself").
Tower of Hanoi

Back in Honours Calculus last year, we studied the Principle of Mathematical Induction and then did an example problem using the Tower of Hanoi.
Here is the basic setup: There are three poles onto which you can place some discs. The discs are of different sizes, and start out at one tower, arranged by width: the widest disc at the bottom and the smallest disc at the top.
The objective is to move all the discs from the first tower to form another tower. Usually, you start off with the discs at the far left and must move them to the far right.
A further objective would be to make as few moves as possible.
Rules: Only one disc (the top-most one) may be moved at a time. No larger disc may be placed atop a smaller disc.
Here is what we found (probably):
| discs: | 0 | 1 | 2 | 3 |
| moves: | 0 | 1 | 3 | 7 |
Let
md be the minimum number of moves, and let
d be the number of discs to be moved. We noticed that
md = 2m(d - 1) + 1 We hypothesized that
md = 2^d - 1 for all non-negative integers
m.
Proof:
1. We shall test the first/best case scenario, where
p = 0.
Plug in values:
m = 2^0 - 1
m = 1 - 1
m = 0 If there are no discs to move, there are no moves to make.
This is true!
2. We shall now test if the following scenarios are true; ie, whether or not
m(d + 1) = 2^(d + 1) - 1 Go!
| m(d + 1) = 2 md + 1 |
|
| m(d + 1) = 2 [ 2^d - 1 ] + 1 | Substitute md = [ 2^d - 1 ] |
| m(d + 1) = 2^(d + 1) - 2 + 1 | Multiply through. There's a common base of 2, so add one to the exponent to simplify. |
| m(d + 1) = 2^(d + 1) - 1 | Hoorays! |
So, by the Principle of Math Induction, we have proved that
md = 2^d - 1 for all non-negative integers of
m. We could even add to the table:
| discs: | 0 |
1 | 2 | 3 | 4 | 5 | . . . | n |
| moves: | 0 | 1 | 3 | 7 | 15 | 31 | . . . | 2^n - 1 |
Sometimes, a story goes with the Tower of Hanoi. There are variations, but the idea is that, at the beginning of the world, there were these monks who had this game set up in their temple. When they had finished the game, the world would end.
Supposing it takes one second to move each plate (not very realistic), and there are 64 discs, when will the world end?
d = 64
m = 2^64 - 1
m = 18 446 744 073 709 551 615So, the world would end in roughly 585.442 billion years. The universe is roughly
13.7 billion years old, +/- 1%. Hehehe.
Being a Teaching AssistantBeing a teaching assistant is conflicting right now. On the one side, it's like job-shadowing, except I get paid--quite well. On the other side, it's incredibly tedious and painful to see what I would consider bad teaching, and not be able to do much about it.
I got such fulfillment today when one student called me over to explain something.
The way I teachWhen a student puts up his hand, I come over. If there is a seat available, I'll sit down; if not, I'll kneel on the ground (this usually puts me just below his eye level). Then I ask, "How can I help you?"
After the student has explained his difficulty, I will confirm that I understand it. This helps me to be clear what I'm trying to do; and also gives me a little thinking time.
I used to be afraid of stuttering, so I'd take silence over stammering or filler. But when I teach, I have to remind myself it's okay to show that I don't know everything or that I'm not infallible; so if I'm having difficulty, I might make a short, "Um," to let him know I'm thinking.
I try to use at least two different methods to explain or solve a problem. I have a habit of asking, "Does that help?" afterward. I think maybe I do this too quickly sometimes; but I found it to be very helpful.
If someone else wants my attention at the same time, usually, I will tell him to wait; because if a student calls for my help, I want to show I am available.
After, if I feel that the student has time or interest, I'll go a little further and tell how it relates to other fields, where else it can be seen, or other cool things that can be done with it.
I think that's all for tonight. I'll just mention that on Tuesday, I'm going to be
enrolled in the Militia. They asked me to bring a small recent photo of myself (photo booth at a mall works well) for my temporary ID card; so I went to the mall, and, wow, not one of those four shots turned out well. At least, I'm identify-able, don't look terrible, and I'm wearing clothes I like.
I'm very excited, though.
--Charissa
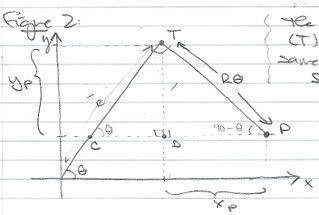
 Involute of a Circle
Involute of a Circle I'm purposely leaving this out, because I can figure it out on my own, thank ye very much!
I'm purposely leaving this out, because I can figure it out on my own, thank ye very much!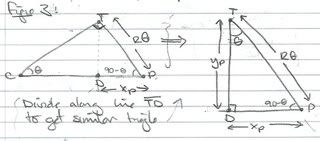

 Thus, the parametric equations for the involute of this circle are:
Thus, the parametric equations for the involute of this circle are: