Involute!

Involute of a Circle

I picked up my Calculus textbook again today, because I was having fun with polar curves and parametric equations.

Man, parametric equations still make me scratch my head sometimes! I get it, it just takes a while to really get what's going on.

Anywho. I came across this problem:

Problem:

A string is wound around a circle and then unwound while being held taut. The curve traced by the point P at the end of the string is called the involute of the circle.

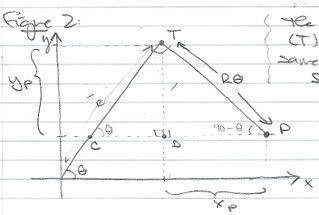
If the circle has a radius r and centre O and the initial position of P is (r, 0), and if the parameter θ is chosen as in the figure, show that the parametric equations of the involute are
...

I'm purposely leaving this out, because I can figure it out on my own, thank ye very much!

The problem also came with the diagram to the left (I made this in Graph but had to define r, so here, r=1).




Solution

The first thing I did was find the path of the point T.

x = r * cosθ

y = r * sinθ

To get the parametric equations for the path of P, something must be added or subtracted to the path of T.

Re-draw the figure as triangles:

The distance from T to P is the same as the arc length for an angle θ. So, that distance is

S = rθ = distance from T to P

I made some reference points:

C := the point on the radius, with same y-value as in point P

D := the point with the x-value of point T and the y-value from point P.

x_p := distance along x-axis, from D to P. Add this to the path of T to get path of P.

y_p := distance along y-axis, from T to C. Subtract this to the path of T to get path of P.

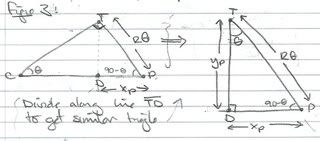
From these new references, start defining the parametric equations for path of P:

x = r * cosθ + x_p

y = r * sinθ - y_p.

Next determine the values of x_p and y_p using the right-hand triangle from above:

From here, we can divide the triangle along line TD to get a similar triangle:

From here, we get:

sinθ = x_p / rθ

x_p = rθ * sinθ

cosθ = y_p / r

y_p = rθ * cosθ.

Plug these back to get:

x = r * cosθ + r * θ * sinθ

x = r (cosθ + θ sinθ)

y = r * sinθ - r * θ * cosθ

y = r (sinθ - θ cos θ).

Thus, the parametric equations for the involute of this circle are:

x = r (cosθ + θ sinθ)

y = r (sinθ - θ cos θ).

When you graph it from 0 ≤ θ ≤ 2πr, it looks something like the blue curve (but here, r=1):


Woots!
--Charissa