Every two months or so, I go kinda crazy--just a little, though. For about five days, I am restless, pouty, petty, dramatic, anxious, confused--all sorts of nasty things. An additional side-effect is that I can believe anything. I won't know waking reality from dreams; I won't know waking reality from things I read; I won't know waking reality from what I want to believe. Added to this, I have a mild fever that's been off and on for about a week.
For anyone who has an idea the state my mind's normally in, you may have an extra appreciation of the mess this stirs up.
Teaching
We've just "finished" teaching Conic Sections to the kids. I'm not sure what he taught, I was marking their papers so they'd know how they're doing before the exam comes.
In S4 Pre-Calculus, we made a flow chart for identifying types of conic sections. I want the students to have it, but I'm not sure what the teacher has in mind.
That being said...
Because Saturday, December 01 is my fitness test with the Army, I might miss part of Math school that day. That's a review class, and I'd be sorry to miss it. One student is even writing the exam that day because he won't be there next week.
Upcoming Saturdays:
December 01
* Here is what I want to talk about on December 15...
Conic Sections
History
Way, way back, circa 200 BC, there was a Greek named Apollonius, and he wrote a book called On Conics. This earned him the title, "The Great Geometer". The study of conics has been around for a long time! (Will add more later.)
What are they?
Imagine two hollow cones placed together at their points, sort-of like an hour-glass. By cutting different 2D sections of this, you get "Conic Sections".
Taking a slice of a cone, parallel to an edge gives a parabola.
Taking a slice of a cone at an angle such that you slice through both halves, gives a hyperbola.
Taking a horizontal slice gives either a circle or a single point (if you cut at the joining point).
Tilting that circular slice gives an ellipse.
Definitions
A circle is the set of all points** equidistant from a single point. To draw one, wrap a loop of string around a pin and a pencil and draw as far from the pin as possible without tilting the pencil.
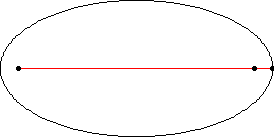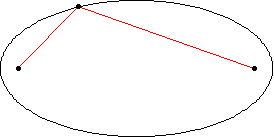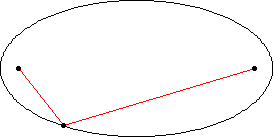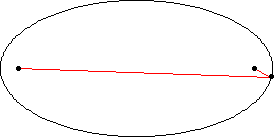
An ellipse is the set of all points** whose distance from both foci is constant (ie: the distance from one point to the first focus plus the distance from the same point to the other focus always adds up to the same number). To draw one, wrap a loop of string around two pins and a pencil and draw as far from the pins as possible.
A parabola is defined as the set of all points** equidistant from a line and a point F (the focus) not on the line (see the right-hand side of this image).
A hyperbola is the set of all points whose distance from one focus, minus the distance to the other focus, is constant.
**(in a plane).
Gravity
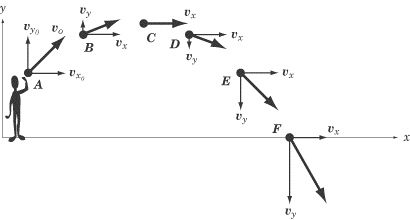The path of a projectile thrown (ie: with another, smaller force in a perpendicular direction) near the surface of the Earth is a parabola. The path the Earth travels around the Sun is an ellipse.
The path of an object (such as a rocket or comet) on an escape trajectory from a fixed mass (such as the Sun) is a hyperbola.
Reflection
The parabola, ellipse and hyperbola each have "focus points" or "foci". If you've ever seen a satellite dish, you have an idea what this means.
For parabolas, an incoming ray that is parallel to the axis of symmetry is reflected toward the focus.
For ellipses, any ray originating at one focus will reflect toward the other focus (this is still true for the special case of the circle, where the "other" focus is the same focus).
Hyperbolas are a bit more complicated. A ray originating from one focus will be reflected and look as though it originated from the other focus (see this image). (There are a few other cases that work out nicely, that I just can't remember right now.)
Light Cone
...Actually, maybe they won't be ready for this yet. But I'll mention it--briefly.
...I should take that book out of the library again...
--Charissa
Further reading:
http://fti.neep.wisc.edu/~jfs/neep602.lecture8.trajectories.97/neep602.lecture8.trajectories.97.html
No comments:
Post a Comment